Turtle Graphics
This project illustrates how to create simple graphics in Lisp using a system called Turtle Graphics, which was originally developed by Seymour Papert as a mathematics teaching tool.
Turtle Graphics is based on controlling a little creature, called the turtle, that moves on the computer's screen. It can respond to a few simple commands, like forward which moves the turtle forward a certain number of units in the direction it is facing, and right which rotates the turtle clockwise a specified number of degrees. The commands back and left cause the opposite movements.
The turtle can leave a trace on the screen as it moves. You can control this with the commands penup and pendown; when the pen is down the turtle draws lines. In the original system the turtle was displayed as a triangular cursor on the screen; in this project the turtle is invisible.
As an example, here's a series of commands to draw a house, and the final result. The turtle starts at the bottom left-hand corner:
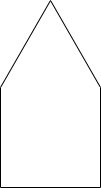
(forward 100) (left 90) (forward 100) (left 30) (forward 100) (left 120) (forward 100) (left 30) (forward 100)
We are going to implement turtle graphics as Lisp procedures, so we can include them in Lisp programs to allow us to make complex plots.
Turtle graphics in Lisp
The first step is to create some global variables to keep track of the window we're plotting on, called turtle-pane, and the turtle's position and angle (in radians):
(defparameter turtle-pane nil) (defparameter turtle-x 320) (defparameter turtle-y 240) (defparameter turtle-theta 0) (defparameter turtle-draw t)
The window will be 640 x 480 pixels, so we've started the turtle in the middle of the window. We'll provide a reset command to reset the turtle's position and heading:
(defun reset () (setf turtle-x 320) (setf turtle-y 240) (setf turtle-theta 0) (setf turtle-draw t))
The LispWorks graphics package provides a command gp:draw-line to draw a line; the format is:
(gp:draw-line pane from-x from-y to-x to-y)
Here's the procedure for forward:
(defun forward (length)
(let ((new-x (+ turtle-x (* length (cos turtle-theta))))
(new-y (- turtle-y (* length (sin turtle-theta)))))
(if turtle-draw
(gp:draw-line turtle-pane turtle-x turtle-y new-x new-y))
(setf turtle-x new-x)
(setf turtle-y new-y)))
We first calculate the new position of the turtle, new-x and new-y, draw a line from the old position to the new position, and finally update turtle-x and turtle-y. The Lisp functions cos and sin give the cosine and sine of their argument in radians.
Here's the procedure for right. We convert the angle to radians since we're keeping turtle-theta in radians:
(defun radians (angle) (* pi (/ angle 180))) (defun right (angle) (setf turtle-theta (- turtle-theta (radians angle))))
The definitions of back and left are pretty simple:
(defun back (length) (forward (- length))) (defun left (angle) (right (- angle)))
Finally penup and pendown:
(defun penup () (setf turtle-draw nil)) (defun pendown () (setf turtle-draw t))
Drawing graphics in a window
Finally, we need the commands to create a window on which we're going to plot the turtle graphics. The main routine, plot, creates an area called a capi:output-pane, and calls capi:contain to display it in a plain window:
(defun plot () (capi:contain (make-instance 'capi:output-pane :display-callback 'draw) :best-width 640 :best-height 480))
When the window is created it calls a procedure draw to draw the graphics. This is where we put the turtle graphics commands. For example, here's the example to draw a house:
(defun draw (pane &optional x y width height) (declare (ignore x y width height)) (setf turtle-pane pane) (reset) (forward 100) (left 90) (forward 100) (left 30) (forward 100) (left 120) (forward 100) (left 30) (forward 100))
The draw procedure takes extra parameters that aren't needed here; the declare ignore line stops these generating an error message when you compile the procedure.
Finally, run the turtle by calling:
(plot)
Now let's look at some more interesting graphics examples.
Inward spiral
An inward spiral is a curve of increasing curvature. We can define it as follows:
(defun inspi (side angle inc count)
(forward side)
(right angle)
(if (> count 0)
(inspi side (+ angle inc) inc (- count 1))))
Here side is the length of each segment of the spiral, angle is the starting angle, inc is the increment to the angle, and count is the number of times we repeat the command (otherwise it would go on forever).
Here's the call to draw for angle=20 and inc=2:
(defun draw (pane &optional x y width height) (declare (ignore x y width height)) (setf turtle-pane pane) (reset) (inspi 50 2 20 1000))
and the result:
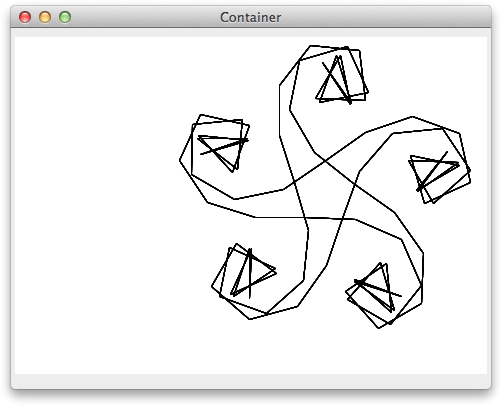
Here are some other values of angle and inc to try:
- angle=0, inc=7
- angle=40, inc=30
It's an interesting mathematical problem to work out why the routine gives the shapes it does in these cases.
Dragon curve
Here's a second example; it's a recursive curve called the dragon curve.
It's defined by two routines; a left-handed version ldragon and a right-handed version rdragon:
(defun ldragon (size level)
(if (= level 0)
(forward size)
(progn
(ldragon size (- level 1))
(left 90)
(rdragon size (- level 1)))))
(defun rdragon (size level)
(if (= level 0)
(forward size)
(progn
(ldragon size (- level 1))
(right 90)
(rdragon size (- level 1)))))
Here's the draw routine to plot the curve of level 11:
(defun draw (pane &optional x y width height) (declare (ignore x y width height)) (setf turtle-pane pane) (reset) (ldragon 4 11))
Finally, here's the result:
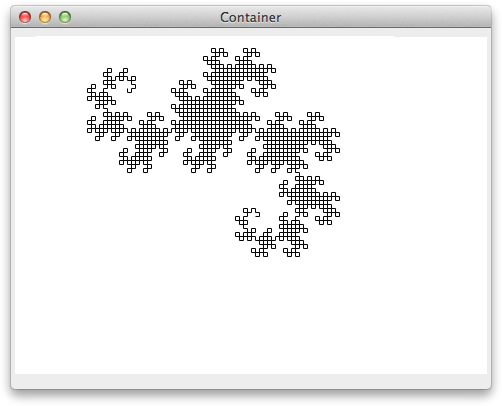
References
For an excellent description of turtle graphics, many other examples that can be directly implemented in Lisp, and the mathematics behind them, see the book Turtle Geometry by Harold Abelson and Andrea DiSessa, MIT Press, 1980, which is still in print.
blog comments powered by Disqus
