More about Recursion
Many problems are solved most elegantly and easily by writing a recursive function - namely, a function that refers to itself. As an example, here's a problem that's very hard to solve without recursion, but which is straightforward using recursion.
Recursion on trees
We have a simple word game where one player names a letter, and the players then take turns in adding a letter to either end to make a new word. The first player unable to make a word loses.
We can represent the possible choices at each stage as a tree (here we only give two alternatives at each stage):
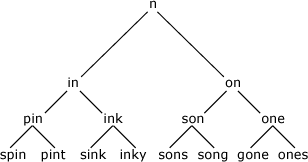
In Lisp we can represent this tree as a list:
(word left-branch right-branch)
When a branch is empty we put nil, so the tree shown above is:
("n" ("in" ("pin" ("spin" nil nil) ("pint" nil nil)) ("ink" ("sink" nil nil)
("inky" nil nil))) ("on" ("son" ("sons" nil nil) ("song" nil nil))
("one" ("gone" nil nil) ("ones" nil nil))))
The tree structure becomes much clearer if we lay out the list on several lines, with indentation:
("n"
("in"
("pin"
("spin" nil nil)
("pint" nil nil))
("ink"
("sink" nil nil)
("inky" nil nil)))
("on"
("son"
("sons" nil nil)
("song" nil nil))
("one"
("gone" nil nil)
("ones" nil nil))))
Now suppose we want to write a procedure print-tree that takes a tree, like the one above, and prints each word on the tree. The problem is a bit tricky until you see the recursive solution; in words:
To print a tree:
- Print the word at the top of the tree
- Print the left branch
- Print the right branch
Here's the definition in Lisp:
(defun print-tree (tree)
(if (null tree) nil
(progn
(print (first tree))
(print-tree (second tree))
(print-tree (third tree)))))
Remember that (first tree) is the word at the top of the tree, (second tree) is the left branch, and (third tree) is the right branch). We use the procedure print-tree itself to print the left branch and right branch.
We run it as follows:
CL-USER 1 > (defparameter tree '("n" ("in" ("pin" ("spin" nil nil) ("pint" nil nil))
("ink" ("sink" nil nil) ("inky" nil nil))) ("on" ("son" ("sons" nil nil)
("song" nil nil)) ("one" ("gone" nil nil) ("ones" nil nil)))))
CL-USER 2 > (print-tree tree) n in pin spin pint ink sink inky on son sons song one gone ones NIL
Recursion with numbers
Here's a second example of using recursion to solve a numerical problem.
The factorial of n is defined as the product of all the numbers from 1 to n: 1 * 2 * 3 * .... * n
You can express this as a recursive definition as follows:
- To find factorial n, find factorial (n-1) and multiply by n.
We need one more piece of information to stop the recursion going on forever:
- The factorial of 1 is 1.
Now we can write the recursive definition of factorial:
(defun factorial (n)
(if (= n 1) 1
(* n (factorial (- n 1)))))
Check it works:
CL-USER 1 > (factorial 10) 3628800
Exercises
1. Count the items on a tree
Write a procedure count-tree that counts the number of items on the tree. Using the tree defined above, check that:
(count-tree tree)
gives 15.
2. Find an item on a tree
Modify print-tree to make a procedure find-tree that checks whether a word is on the tree.
Using the tree defined above, check that:
(find-tree tree "gone")
gives T, and:
(find-tree tree "tins")
gives NIL.
3. Find the nth fibonacci number
The fibonacci sequence is:
1 1 2 3 5 8 13 21 34
where the first two terms are 1, and each subsequent term is the sum of the two previous terms.
Write a recursive function fib that returns the nth fibonacci number.
Check that:
(fib 10)
gives 55.
4. Find a specified number on Pascal's triangle
Pascal's triangle begins:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
where each number is the sum of the two numbers above it. Write a function that gives the nth number in the rth row. For example:
(pascal 3 5)
should give 6.
blog comments powered by Disqus
