Logic Mazes
Logic Mazes are puzzles in which the task is to find a route through the maze according to certain logical rules. A popular type of logic maze is the Jumping Maze (also sometimes called a Number Maze) in which each cell contains a number telling you how far you can jump to the next cell.
Here's a typical Jumping Maze, called Chain Reaction. You start in the top left corner, and you have to find the shortest route to the bottom right corner by making just horizontal or vertical jumps:
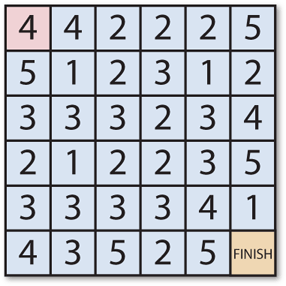
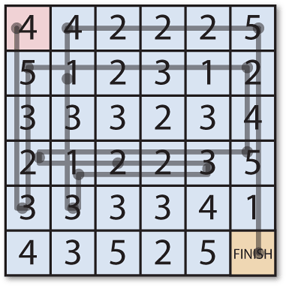
For example, from the 4 at the start you can jump to the rightmost 2 in the first row, or the bottom 3 in the leftmost column, and so on:
In this project we'll write a Lisp program to solve an arbitrary jumping maze.
Representing the maze
We'll number the cells in the maze starting from 0 in the top left corner, so in this example the final cell is 35.
The maze will be represented as a list of numbers; in this case the maze is:
(defparameter maze
'(4 4 2 2 2 5
5 1 2 3 1 2
3 3 3 2 3 4
2 1 2 2 3 5
3 3 3 3 4 1
4 3 5 2 5 0))
Four further parameters specify the start, goal, and size of the maze:
(defparameter start 0) (defparameter goal 35) (defparameter width 6) (defparameter height 6)
Working out the available moves
The next step is to work out the available moves from each square. The procedure parse-board returns a list of cells you can get to from each of the cells in the maze; for this maze it is as follows:
CL-USER > (parse-board maze width height) ((4 24) (5 25) (0 4 14) (1 5 15) (2 16) (0 35) (11) (6 8 13 1) (6 10 20) (6 27)
(9 11 16 4) (9 23) (15 30) (16 31) (17 32) (13 17 27 3) (13 34) (13) (20 30 6)
(18 20 25 13) (18 22 32 8) (19 23 33 9) (19 4) (18) (27 6) (28 7) (29 8) (24 9)
(24 4) (28 35 23) (34 6) (34 13) (2) (31 35 21) (4) NIL)
For example, the first element in this list, (4 24), means that you can reach cells 4 and 24 from the starting cell.
The procedure scans across each row and column of the maze, and for each cell calculates the destination cell in each of the four directions. It tests whether the destination is a valid square on the board with:
(and (< -1 x) (< x size-x) (< -1 y) (< y size-y))
If so, it adds the cell to the list of moves.
We store this list of valid moves in the global parameter moves:
(defparameter moves (parse-board maze width height))
Representing the current state
As we search for a route through the maze we will use a list to store the current cell number, and the route taken so far. For example, after visiting cells 0 4 and 16 the state will be:
(16 (4 0))
The procedure next-moves takes the current state as a parameter, and returns a list of states corresponding to each of the cells you can reach from the current cell:
(defun next-moves (state)
(let* ((cell (first state))
(route (second state))
(result nil))
(dolist (move (nth cell moves))
(setf result (cons (list move (cons cell route)) result)))
result))
Here's an example
CL-USER > (next-moves '(16 (4 0))) ((34 (16 4 0)) (13 (16 4 0)))
In other words we can reach cells 34 or 13 from cell 16.
Finally, tree-search calls next-moves to follow every possible route through the maze until it reaches the specified goal:
(defun tree-search (states)
(if (null states)
nil
(if (= (first (first states)) goal)
(reverse (cons (first (first states)) (second (first states))))
(tree-search
(append (rest states)
(next-moves (first states)))))))
The logic of this procedure is as follows:
- If the list of states is empty there is no solution, so stop.
- If the first item in the list of states has reached the goal, return the route we've found.
- Otherwise continue searching the rest of the states, followed by the cells you can reach from the first state.
Because we check the shortest routes first, before extending them with the next moves, this approach (called a breadth-first search) succeds in finding the shortest route through the maze.
Running the program
Finally, we can run the program by calling:
CL-USER > (tree-search (list (list start nil)))
This starts the search with a list containing the start cell and an empty route. The result comes back:
(0 24 6 11 23 18 20 22 19 25 7 1 5 35)
which gives us the solution to the maze!
Extending the project
Diagonal moves
Some jumping mazes also allow you to move diagonally, in addition to horizontally or vertically. Accomodating this rule is simply a matter of changing the appropriate line in parse-board to include diagonal moves:
(dolist (d '((0 -1) (0 1) (1 0) (-1 0) (-1 -1) (-1 1) (1 -1) (1 1))
References
You can find more jumping mazes, and other types of logic maze, at my logic maze site, Mazelog:
Some of the most impressive jumping mazes (or number mazes) have been designed by game and maze designer Robert Abbott. You can find several on his web site; for example:
http://www.logicmazes.com/n1mz.html
blog comments powered by Disqus
